| Home | Notes | Github |
|---|
Written on the last train home, 20-Jan-2023 (Fixed 22-Jan-23)
This is my solution to the ain’t it funny how the knight moves problem.
It’s an interesting puzzle, but try it now before I (hopefully) reveal some of its underlying structure.
After getting a couple successfully - in about 10 minutes, - I noticed several squares are dead ends, and others are pretty common. My hypothesis here was that there was a couple of paths, and one or two spots to transfer between them. To test this I thought looking at an abstracted network of nodes would be the best way. And if nothing else, it’ll be a cheat sheet to complete the rest of the puzzle.
So a quick mo’ of graphviz-ing later, here’s what we get:
So I was sort of right, but more wrong.
My first impression is I’m shocked it’s symmetrical, given the asymmetry of the queens location. That said it’s chess so it shouldn’t be that surprising. Esp. given the first few tries were asymmetrical (I wrote the graph when tired on a train), after fixing the mistakes it was cool to see this symmetry appear.
So regarding the hypothesis… There are clear loops that can be followed, but more interlinking than expected, and not the clearly obvious 2 transfer nodes.
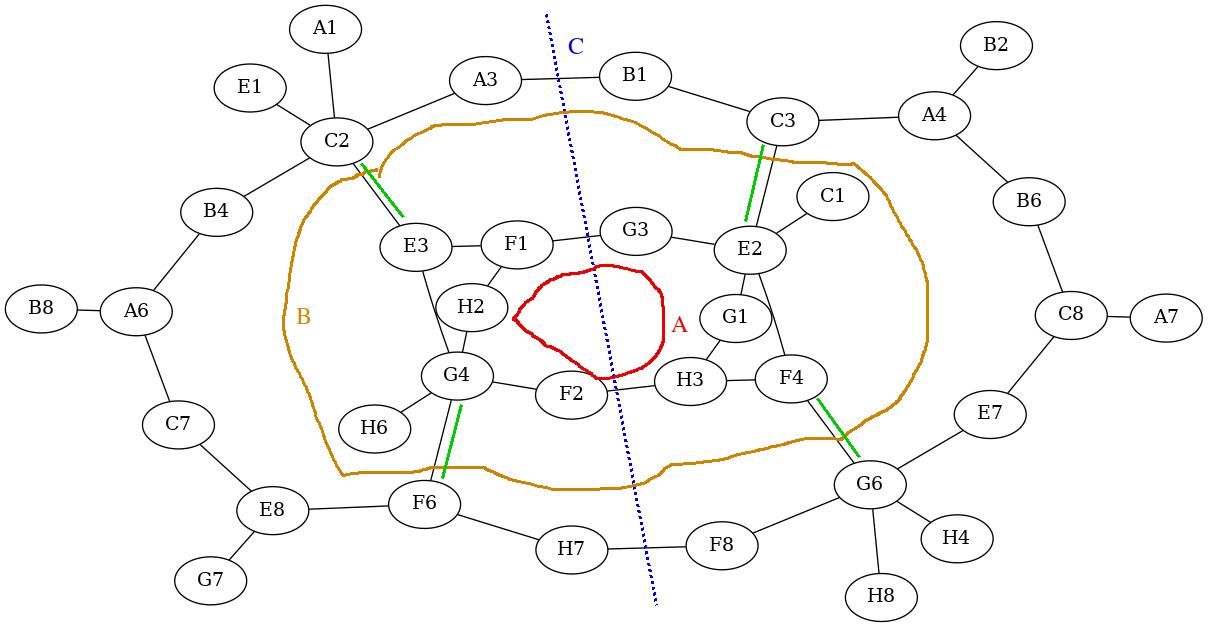
However that said, there are some interesting things of note. I’ve marked up the graph into an image below1 to help with explaining. So there are lots of loop, but the apparently key loop is the red one marked “A” and it’s well connected small loop. Well connected because its only a 2 moves away from the majority of the board, and 5 from the furthest2.
The best connected spots are G6 and C2 with 5 connections each. If my original hypothesis was correct these would be a key transfer point, and although useful, it’s not pivotal to solving the puzzle. Only six points would be inaccessible3 (<20% of accessible) if you didn’t have them: H4, H8, A1, E1 and of course G6 and C2 themselves. What is interesting is thatthere are constrictions to get between differnt loops in the graphs. Bettween the two halves (seerated by the blue line marked “C”) there are only four links. And between the inner loop “A” and the outer loop (seperated by orange line “C”) there are only four connection points (marked with the green lines). This inner-outer split on the graph is almost another 50-50 split, wiht 14 nodes inside Interestingly C2 and G6 are on these lines
highlighted in blue) between the well connected half (Enclosed by the orange line “B”) and the “Outer Loop” of points. One of these interconnects is the aforementioned G6, but there are three others (E2, E3 and F6). So I was partially right, because there were limited places to jump between loops, but more than I anticipated.
Regarding dead ends, there are clearly plenty (9 which is 25% of accessible squares), and fairly well dispersed. However another sub-hypotheses I didn’t mention was I thought there’d be one or more “2 step dead ends”, where you’d go to one spot, where there’d only be one other available space to go to, which would itself be a dead end. This would appear in the graph as a node with only two connections (plenty of those) but one would be a dead end (none of those). This means that you don’t have to go far off one of the loops to get to where you need to get to.
So I hadn’t actually played the game to it’s conclusion yet.
Notably - at least from the initial stages - it felt like a lot of it was about navigating the wider ring, to go to difficult to get spots. This is not surprising given that this is a puzzle, and wasn’t designed to be an easy “A to B” journey. This meant there were many steps going from A6 to A7 right across the map, despite being a tile away.
I’d be interested in seeing how the creator of the puzzle made this. It seems that each move goes quite far away from the previous, but is never (or rarely) the furthest away spot. So maybe the creator was looking at a similar graph to pick the move order, or maybe they looked at knights tours for inspiration, or maybe yet they’re a chess genius, or even just trial and error and play testing did it. Either way I found it was a thought provoking puzzle.
Note: So it turns out - although not visible on mobile - Jair Trejo (the puzzle creator) and his inspiration inspiration are visible, but you can look that up yourself there.
For reference (image was generated using sfdp) :
graph D {
overlap = false;
splines = true;
A1 -- C2
B1 -- {A3, C3}
C1 -- E2
E1 -- C2
F1 -- {E3, G3, H2}
G1 -- {E2, H3}
B2-- A4
C2 -- {A3, B4, E3}
E2 -- {C3, F4, G3}
F2 -- {G4, H3}
H2 -- G4
C3 -- A4
E3 -- G4
H3 -- F4
A4 -- B6
B4 -- A6
F4 -- G6
G4 -- {F6, H6}
H4 -- G6
A6 -- {B8, C7}
B6 -- C8
F6 -- {E8, H7}
G6 -- {E7, F8, H8}
A7 -- C8
C7 -- E8
E7 -- C8
G7 -- E8
H7 -- F8
}